
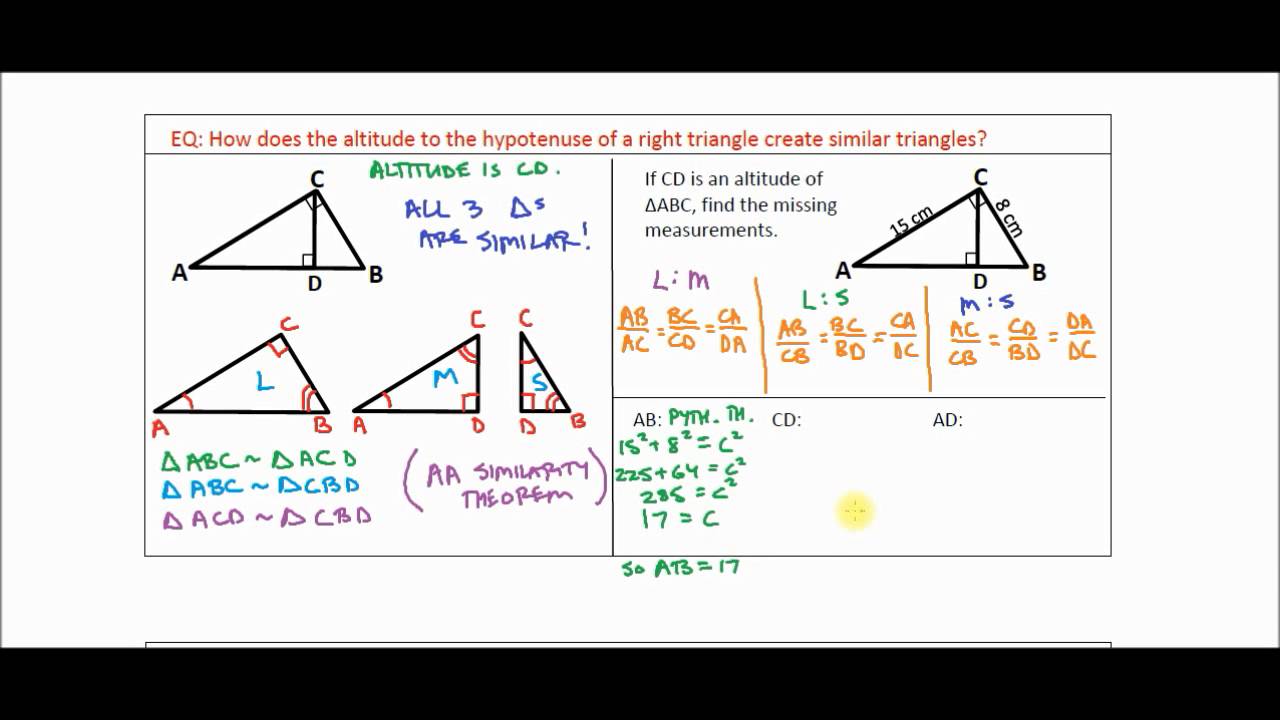
Step 1: Given a right triangle, the altitude from the right angle to the hypotenuse divides the triangle into 2 smaller right triangles. Check it out!!! A surveyor positions himself so that his line of sight to the top of a cliff and his line of sight to the bottom form a right angle as shown. Steps to Identify Similar Right Triangles that Overlap.
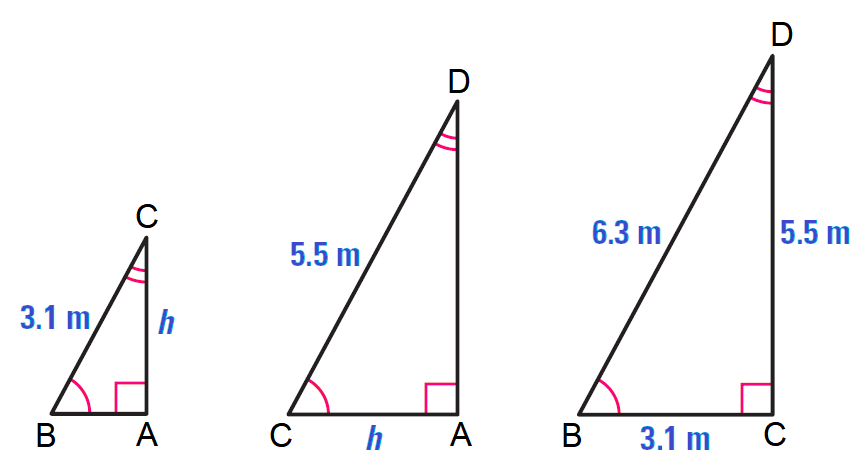
What is the height of the tree to the nearest meter? The tree is about 38 + 1.6 = 39.6, or 40 m tall Similar Right triangles: Two right triangles are similar if the corresponding sides are proportional to each other, and the corresponding angles are congruent. Her eyes are about 1.6 m above the ground, and she is standing 7.8 m from the tree. Explore the relationship between the two triangles. Example 4: Measurement Application To estimate the height of a Douglas fir, Jan positions herself so that her lines of sight to the top and bottom of the tree form a 90 angle. Divide a right triangle at the altitude to the hypotenuse to get two similar right triangles.Check It Out! Example 3 Find u, v, and w.Example Example 3: Finding Side Lengths in Right Triangles Find x, y, and z.All the relationships in red involve geometric means. Similarity in right triangles You can use Theorem 8-1-1 to write proportions comparing the side lengths of the triangles formed by the altitude to the hypotenuse of a right triangle.
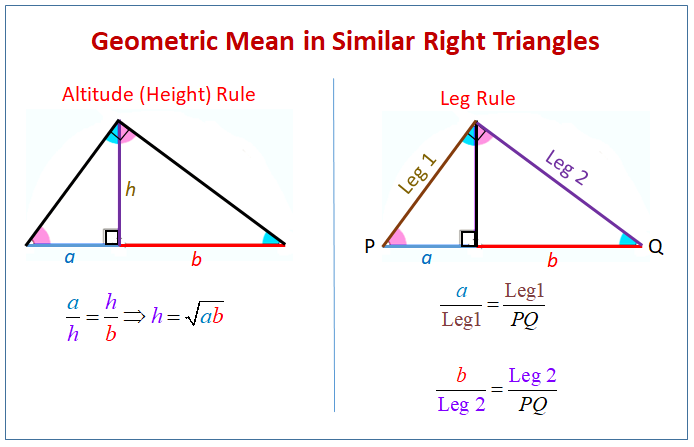
If necessary, give the answer in simplest radical form. Check it out!! Find the geometric mean of each pair of numbers.Example Find the geometric mean of each pair of numbers. Two triangles are similar if the ratio of corresponding sides is is constant and the corresponding angles are equal.4 and 25 Solution Let x be the geometric mean. Example 2A: Finding Geometric Means Find the geometric mean of each pair of numbers.So the geometric mean of a and b is the positive number x such that, or x 2 = ab. The geometric mean of two positive numbers is the positive square root of their product. In this case, the means of the proportion are the same number, and that number is the geometric mean of the extremes. Geometric mean Consider the proportion. Theorem If an altitude is drawn to the hypotenuse of a Right triangle, then it makes similar triangles to the original Right.Check it out Write a similarity statement comparing the three triangles By Theorem 8-1-1, LJK ~ JMK ~ LMJ.Solution Sketch the three right triangles with the angles of the triangles in corresponding positions.Example #1 Write a similarity statement comparing the three triangles.Similarity in right triangles In a right triangle, an altitude drawn from the vertex of the right angle to the hypotenuse forms two right triangles.Apply similarity relationships in right triangles to solve problems. Objectives Use geometric mean to find segment lengths in right triangles.Chapter 8 8-1 Similarity in right triangles.The Similarity between triangles is denoted by ” ∼ ”Īll similar triangles may or may not be congruent. The congruency between triangles is denoted by ” ≅ “. Similar figures have the same shape but may or may not have the same size. If one angle of a triangle is equal to one angle of other triangles and the sides including these angles are proportional, then the triangles are said to be similar.ĭifference between Similarity and congruency of triangles CongruencyĬongruent figures have the same shape and same size. Let us elaborate and understand this concept.Īlso, the ratio of these proportional sides should be equal. “Two triangles are said to be similar if their corresponding sides are proportional and corresponding angles are equal.”
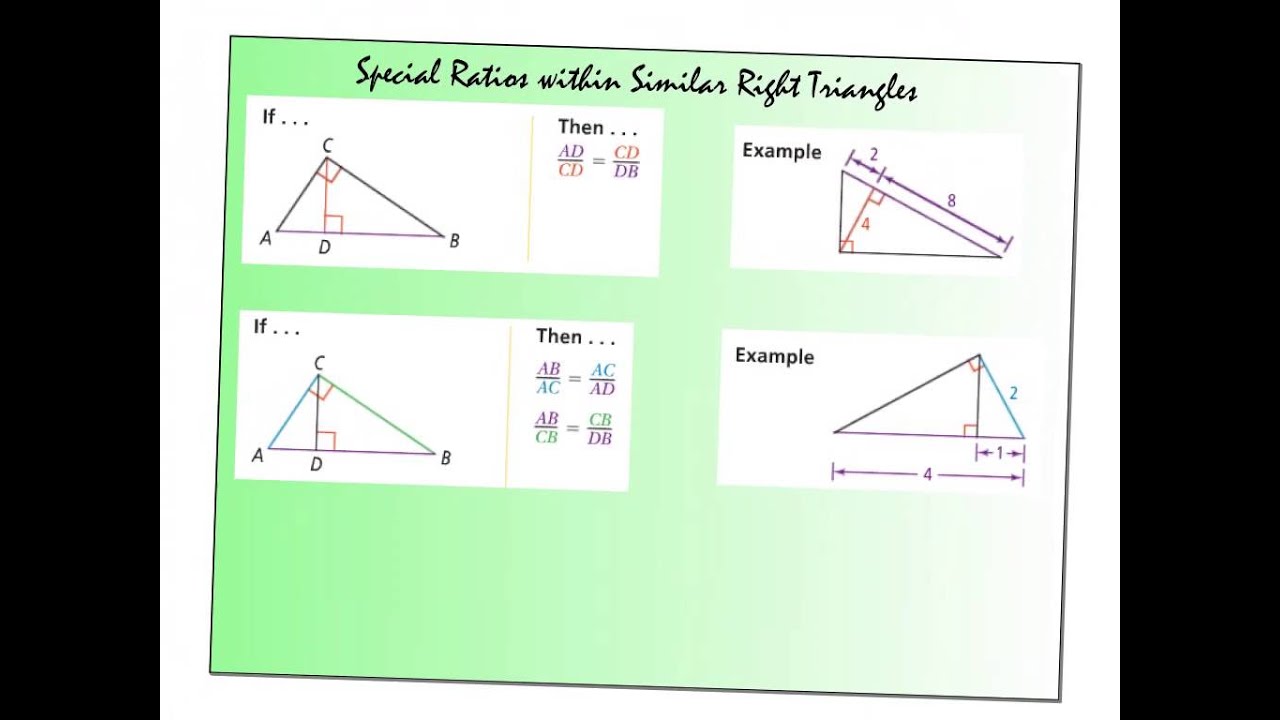
When two figures have the same shape but do not necessarily have the same size, then they are called similar figures. This section deals with the concept of Similar triangles and different criteria for the similarity of triangles. If we in the following triangle draw the altitude from the vertex of the right angle then the two triangles that are formed are similar to the triangle we. Cut the paper on the diagonal to make two congruent right triangles. And Why To nd a distance indirectly, as in Example 3 11 Using Similarity in Right Triangles Hands-On Activity: Similarity in Right Triangles Draw one diagonal on a rectangular sheet of paper.


 0 kommentar(er)
0 kommentar(er)
